Du calcul approximatif au calcul symbolique
Lors de l’apprentissage du calcul symbolique (qui s’appuie sur l’utilisation de symboles numériques), les enfants “recyclent” leurs capacités de calcul approximatif et associe au système pré-existant les symboles des nombres (Dehaene 2004).
Les tâches qui passent par la manipulation de quantités (additions, soustractions, multiplications, comparaisons, etc) activent toutes la même région du sillon intrapariétal dans le cerveau, qui est le noyau du système numérique principal (cf. Le “triple code” [lien interne vers les bases cérébrales du calcul]).
D’autre part, les différents types de calcul semblent s’appuyer sur des circuits cérébraux relativement distincts au sein de l’architecture du “triple code” :
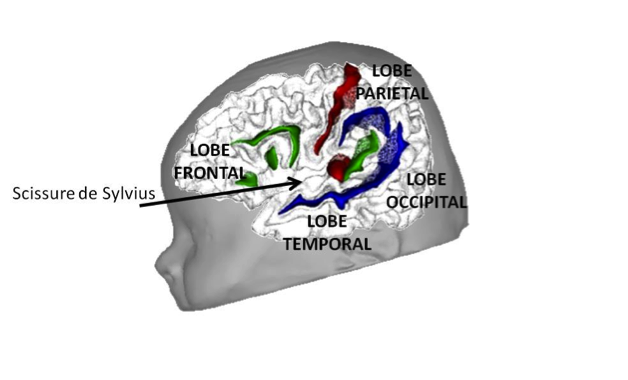
le gyrus angulaire gauche et le cortex perisylvien présentent une activation plus importante lors d’un calcul exact, et d’autant plus qu’il repose fortement sur la mémoire verbale “par coeur” (par exemple, l’utilisation de tables de multiplication ou la résolution d’additions basiques) : cela est probablement lié au fait que ce type de mémorisation existe dans la plupart des cultures (Dehaene 1999, Lee 2000, Venkatraman 2006).
Le calcul
A l’origine, le calcul est un processus extrêmement exigeant en termes de concentration, de mémoire de travail et donc de ressources cognitives.
Différentes stratégies peuvent être utilisées lors de la résolution d’opérations :
la plupart des jeunes enfants commencent par utiliser leurs doigts pour compter ;
ils passent graduellement au comptage verbal,
puis à la décomposition
et enfin aux procédures de récupération en mémoire des opérations qu’ils ont apprises.
Bien que tous les types de calcul s’opèrent par l’accès au ‘système numérique principal’, les opérations arithmétiques complexes reposent aussi profondément sur les circuits et mécanismes visuo-spatiaux, et les résultats arithmétiques appris par cœur (comme les tables de multiplication) dépendent plus de la mémoire verbale.
De l’hémisphère droit à l’hémisphère gauche
Étonnamment, pendant l’apprentissage, l’activation cérébrale liée aux quantités et au calcul passent petit-à-petit de l’hémisphère droit à l’hémisphère gauche : au fur et à mesure, la région intrapariétale gauche gagne en précision sur son homologue droite et s’active plus lors des calculs exacts (Piazza 2004), probablement à cause du rôle qu’y joue le langage, au contraire des calculs approximatifs qui recrutent moins ce dernier (Spelke 2001).