Ce texte de Jessica Sendef et Arryn Robins publié dans Frontiers for Young Minds en septembre 2019, a été traduit et adapté de l’anglais par S.Desmidt, Marie Palu et G. Dehaene-Lambertz.
Résumé
Des études montrent qu’une personne pose environ 20 questions par jour en moyenne! Bien sûr, certaines de ces questions peuvent être simples, comme demander à votre professeur si vous pouvez aller aux toilettes, mais d’autres peuvent être complexes et la réponse difficile à trouver, comme “ce médicament est-il efficace dans cette maladie”? C’est pour ces questions que les statistiques sont utiles car elles permettent de tirer des conclusions à partir d’un échantillon de données. Les statistiques sont donc la “science des données”. Elles sont utilisées dans tous les secteurs d’activité pour répondre à des questions de recherche ou d’affaires. Par exemple, elles peuvent aider à prédire quelle vidéo vous aimeriez regarder à partir de celles que vous avez déjà regardées. Mais pour les spécialistes des sciences sociales et les psychologues, les statistiques sont un outil indispensable pour répondre aux questions de recherche.
POSER DES QUESTIONS DE RECHERCHE
Les scientifiques posent de nombreuses questions auxquelles les statistiques permettent de répondre. Par exemple, un psychologue pourrait s’intéresser à la manière dont les performances d’un test sont affectées par la quantité de sommeil de l’élève la veille du test. Le type d’analyse statistique effectué dépend de la question posée et des variables mesurées. Les variables sont des facteurs, des traits ou des conditions qui peuvent être continus (comme la taille) ou discrets (comme le sexe, masculin ou féminin).
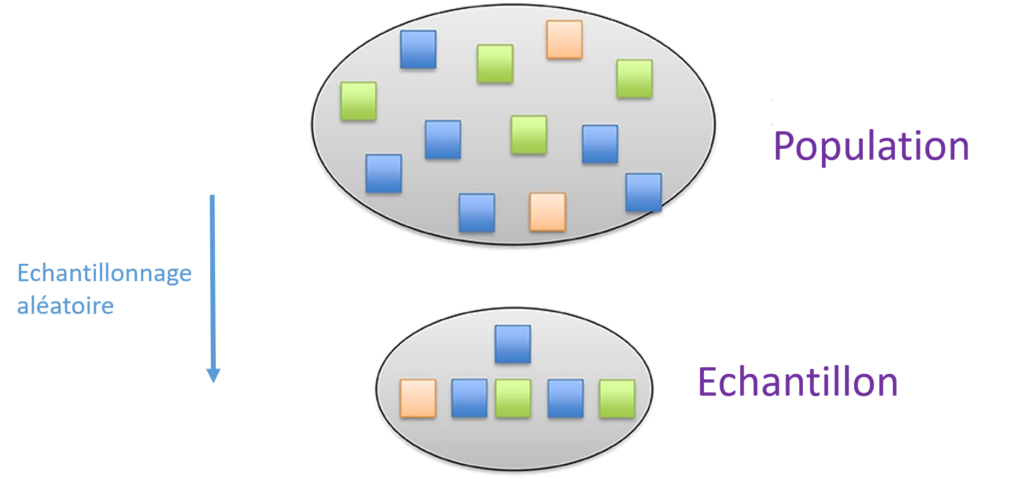
Dans l’échantillonnage aléatoire, chaque individu de la population a une chance égale d’être sélectionné pour l’échantillon. Dans cet exemple, chaque couleur de la population est également présente dans l’échantillon, et les proportions de chaque couleur sont représentées de façon similaire dans l’échantillon.
L’ÉCHANTILLONNAGE D’UNE POPULATION
Pour répondre à une questions de recherche, il n’est souvent pas possible de recueillir des informations auprès de tous les membres de la population concernée. Par exemple, pour savoir si le sommeil affecte les résultats des tests, il est impossible de recueillir des informations sur le sommeil et les résultats des tests de tous les élèves du monde ! C’est pourquoi les données sont recueillies auprès d’un échantillon d’individus qui doivent représenter au mieux la population, et donc que les caractéristiques de l’échantillon soient similaires à celles de l’ensemble de la population. Par exemple, les chercheurs s’assurent que les échantillons comportent les mêmes groupes d’âge ou les mêmes groupes ethniques que l’ensemble de la population (Figure 1).
Par exemple, un vétérinaire est intéressé par le calcul du poids moyen de tous les chiens, il pèse cinq chiens, calcule le poids moyen de son échantillon et conclut que le poids moyen de tous les chiens se situe entre 4,5 et 7 kg. Si vous êtes un amoureux des chiens, vous soupçonnez que ce chiffre n’est pas correct. Certains chiens sont gros, et donc la moyenne devrait être plus élevée. Et si le vétérinaire n’avait pesé que des chihuahuas ? Dans ce cas, il ne peut certainement pas dire que tous les chiens pèsent entre 4,5 et 7 kg, mais seulement que les chihuahuas pèsent entre 4,5 et 7 kg. Cet échantillon ne contenant qu’une seule race n’est pas représentatif de tous les types de chiens. Donc le vétérinaire aurait dû d’abord s’assurer que son échantillon représente bien la population qu’il veut mesurer.
L’échantillonnage aléatoire est une méthode essentielle de sélection des individus d’un échantillon. Les scientifiques utilisent l’échantillonnage aléatoire pour garantir que chaque individu de la population a une probabilité égale d’être sélectionné. Cela permet de s’assurer que l’échantillon est similaire à la population globale.
L’ESTIMATION À PARTIR D’UN ÉCHANTILLON
Une fois que le scientifique a rassemblé l’échantillon, il ou elle peut vouloir tirer des conclusions sur cet échantillon et généraliser les résultats à l’ensemble de la population. Par exemple, un scientifique peut vouloir connaître le nombre moyen d’heures de sommeil des enfants de 12 ans chaque nuit, ou la taille moyenne des lycéens aux États-Unis. Afin d’estimer la valeur d’une variable dans une population (comme la taille moyenne), les scientifiques calculent une estimation ponctuelle à partir de l’échantillon. Une estimation ponctuelle est un nombre qui permet d’estimer la valeur réelle d’une variable dans une population, souvent il s’agit d’une moyenne. Par exemple, si nous voulons connaître le nombre moyen d’enfants par ménage dans la ville de Chicago, nous rassemblons un échantillon aléatoire de familles à Chicago et nous demandons à chaque famille combien d’enfants vivent dans leur maison. Ensuite, en utilisant ces informations, nous calculons le nombre moyen d’enfants de ces maisons pour obtenir notre estimation ponctuelle. Nous pouvons alors supposer que le nombre moyen d’enfants dans notre échantillon est très similaire au nombre moyen d’enfants dans toutes les familles de Chicago (figure 2).

Les méthodes d’échantillonnage ne peuvent donner que des mesures partielles, c’est pourquoi les scientifiques utilisent des intervalles de confiance autour des estimations ponctuelles, pour indiquer l’intervalle de valeurs qui contient probablement la vraie moyenne d’une variable dans la population. Pour calculer l’intervalle de confiance, le scientifique doit d’abord calculer l’erreur standard. Cette erreur standard est ajoutée et soustraite d’une estimation ponctuelle. C’est une façon de représenter numériquement les erreurs de calcul et les erreurs d’échantillonnage de la population.
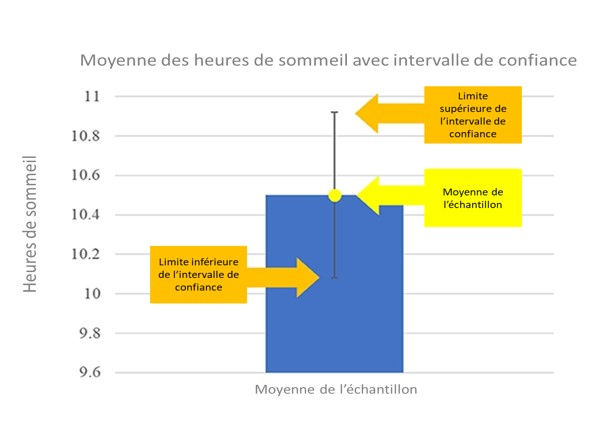
Comment calculer un intervalle de confiance? Imaginons que nous avons rassemblé un échantillon de 49 élèves pour une étude sur le sommeil, et que nous constatons que la durée moyenne de sommeil des élèves est de 10,5 heures (notre estimation ponctuelle). Ensuite, nous devons déterminer l’écart type, c’est à dire la distance moyenne entre chaque mesure de chaque individu et la moyenne du groupe. Lorsque l’écart-type est faible, cela signifie que chaque individu est proche de la moyenne, et un grand écart-type signifie que les différences entre individus sont plus étalées. Dans notre échantillon, l’écart-type est de 1,5 h. Nous pouvons alors calculer la marge d’erreur à l’aide de cette formule :

Dans cette formule, s représente l’écart-type (1,5 h) et n se réfère au nombre de points de données de notre échantillon (49 élèves). Si nous remplaçons les symboles par leurs valeurs correspondantes, nous calculons que notre marge d’erreur est de 0,42 h de sommeil. Nous ajoutons et soustrayons la marge d’erreur de notre estimation ponctuelle pour obtenir les limites inférieure et supérieure de l’intervalle de confiance. Les psychologues utilisent généralement un intervalle de confiance de 95% pour calculer la marge d’erreur (cela correspond à la valeur 1.96 dans la formule), ce qui signifie que nous pouvons être sûrs que, 95% du temps, notre intervalle de confiance contient la moyenne réelle de la population. Notre intervalle de confiance pour l’estimation ponctuelle dans notre exemple serait de 10,5 ± 0,42 h, c’est à dire entre 10,08 et 10,92 h. Cela signifie que, dans 95% des cas, le nombre d’heures de sommeil des élèves dans la population se situe entre 10,08 et 10,92 h (figure 3).
Les scientifiques peuvent réduire la marge d’erreur de plusieurs façons pour rendre leur estimation de la population plus précise. L’une d’elles est d’inclure davantage d’individus dans l’échantillon, de manière à ce que celui-ci soit plus représentatif de la population. Une autre est de s’assurer que la collecte des données est aussi exempte d’erreurs que possible afin de réduire la variabilité des données, par exemple en veillant à ce que tous les outils de mesure (comme les échelles, les enquêtes, les règles, etc.) soient précis dans ce qu’ils mesurent. Plus l’échantillon représente précisément la population, en utilisant un échantillonnage aléatoire et plus la collecte de données est fiable, plus la marge d’erreur est faible et plus l’intervalle de confiance est précis et permet d’estimer au mieux la valeur réelle dans la population.
POSER DES QUESTIONS DE RECHERCHE PLUS COMPLEXES
Parfois, les scientifiques veulent aller au-delà de la description de simples mesures comme la taille moyenne ou la durée de sommeil de la population. Disons que nous ne sommes pas seulement intéressés par la quantité de sommeil des élèves, mais nous voudrions aussi savoir si la quantité de sommeil affecte les performances aux tests que ceux-ci vont passer. La taille de l’effet est une valeur qui permet d’estimer l’ampleur d’un phénomène, ou d’estimer comment une variable (comme les heures de sommeil) influe sur une autre variable (comme les résultats des tests). Par exemple, si le fait de ne dormir que 3 h diminue seulement de quelques points la note des tests par rapport à 9 h de sommeil, il vaut mieux peut-être réviser que dormir. Cependant, si quelques heures de sommeil en moins, font chuter les performances des élèves de manière importante, vous devriez dormir.
Il existe différentes façons de calculer la taille de l’effet, selon la question de recherche et le type de statistiques utilisées par un scientifique. Une fois qu’un scientifique a calculé la taille de l’effet, il peut déterminer si l’effet est petit, moyen ou grand. La taille de l’effet permet au scientifique, ainsi qu’aux autres personnes qui examinent les résultats, de mieux comprendre les effets que certaines variables ont sur d’autres variables de la population.
CONCLUSIONS
Les statistiques dont nous avons parlé dans cet article correspondent à celles utilisées le plus souvent en sciences sociales pour répondre à des questions simples sur la population générale à partir d’échantillons. Mais il existe toute une science des statistiques permettant de décrire les phénomènes scientifiques dans différents domaines. Les statistiques aident les médecins à savoir si tel ou tel médicament peut guérir telle ou telle maladie. Elles aident les ingénieurs à assurer la sécurité du véhicule dans lequel vous roulez. Cela ne s’arrête pas là ; il y a une infinité de questions auxquelles nous pouvons répondre grâce aux statistiques.
Glossaire
Population : Un groupe d’individus identifiés que les scientifiques veulent étudier.
Variable : Facteur, trait ou condition qui est mesuré dans le cadre de la recherche.
Échantillonnage aléatoire : Une façon de sélectionner des individus dans une population qui garantit que chaque individu a une probabilité égale d’être sélectionné.
Estimation ponctuelle : Estimation d’une certaine valeur dans une population, comme une moyenne.
Intervalle de confiance : Intervalle de valeurs autour de l’estimation ponctuelle, qui contient probablement la valeur réelle d’une variable dans la population générale.
Marge d’erreur : Une valeur calculée ajoutée et soustraite à une estimation ponctuelle, qui est prise en compte en cas d’erreur de calcul.
Écart-type : distance moyenne entre chaque point de données et la moyenne.
Taille de l’effet : mesure de la force de l’effet observé.





